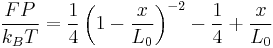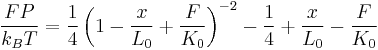Worm-like chain
The worm-like chain (WLC) model in polymer physics is used to describe the behavior of semi-flexible polymers; it is sometimes referred to as the Kratky-Porod model.
Contents |
Theoretical Considerations
The WLC model envisions an isotropic rod that is continuously flexible;[1][2][3] this is in contrast to the freely-jointed chain model that is flexible only between discrete segments. The worm-like chain model is particularly suited for describing stiffer polymers, with successive segments displaying a sort of cooperativity: all pointing in roughly the same direction. At room temperature, the polymer adopts a conformational ensemble that is smoothly curved; at 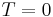 K, the polymer adopts a rigid rod conformation.[1]
K, the polymer adopts a rigid rod conformation.[1]
For a polymer of length 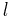 , parametrize the path of the polymer as
, parametrize the path of the polymer as 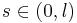 , allow
, allow 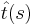 to be the unit tangent vector to the chain at
to be the unit tangent vector to the chain at  , and
, and 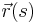 to be the position vector along the chain. Then
to be the position vector along the chain. Then
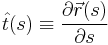 and the end-to-end distance
and the end-to-end distance 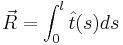 .[1]
.[1]
It can be shown that the orientation correlation function for a worm-like chain follows an exponential decay:[1][3]
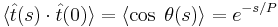 ,
,
where  is by definition the polymer's characteristic persistence length. A useful value is the mean square end-to-end distance of the polymer:[1][3]
is by definition the polymer's characteristic persistence length. A useful value is the mean square end-to-end distance of the polymer:[1][3]
![\begin{matrix}
\langle R^{2} \rangle & = & \langle \vec R \cdot \vec R \rangle \\ \\
\ & = & \langle \int_{0}^{l} \hat t(s) ds \cdot \int_{0}^{l} \hat t(s') ds' \rangle \\ \\
\ & = & \int_{0}^{l} ds \int_{0}^{l} \langle \hat t(s) \cdot \hat t(s') \rangle ds' \\ \\
\ & = & \int_{0}^{l} ds \int_{0}^{l} e^{-\left | s - s' \right | / P} ds' \\ \\
\ \langle R^{2} \rangle & = & 2 Pl \left [ 1 - \frac {P}{l} \left ( 1 - e^{-l/P} \right ) \right ]
\end{matrix}](/2012-wikipedia_en_all_nopic_01_2012/I/77c4bf259a478c95b3acf87353ae4fda.png)
- Note that in the limit of
 , then
, then 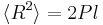 . This can be used to show that a Kuhn segment is equal to twice the persistence length of a worm-like chain.[2]
. This can be used to show that a Kuhn segment is equal to twice the persistence length of a worm-like chain.[2]
Biological Relevance
Several biologically important polymers can be effectively modeled as worm-like chains, including:
Stretching Worm-like Chain Polymers
Laboratory tools such as atomic force microscopy (AFM) and optical tweezers have been used to characterize the force-dependent stretching behavior of the polymers listed above. An interpolation formula that describes the extension  of a WLC with contour length
of a WLC with contour length 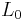 and persistence length
and persistence length  in response to a stretching force
in response to a stretching force  is
is
where 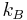 is the Boltzmann constant and
is the Boltzmann constant and  is the absolute temperature (Bustamante, et al., 1994; Marko et al., 1995).
is the absolute temperature (Bustamante, et al., 1994; Marko et al., 1995).
In the particular case of stretching DNA in physiological buffer (near neutral pH, ionic strength approximately 100 mM) at room temperature, the compliance of the DNA along the contour must be accounted for. This enthalpic compliance is accounted for by adding a stretch modulus 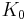 to the above relation:
to the above relation:
where a typical value for the stretch modulus of double-stranded DNA is around 1000 pN and 45 nm for the persistence length (Wang, et al., 1997).
See also
References
- ^ a b c d e Doi and Edwards (1999). The Theory of Polymer Dynamics.
- ^ a b Rubinstein and Colby (2003). Polymer Physics.
- ^ a b c d Kirby, B.J.. Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices. http://www.kirbyresearch.com/textbook.
- ^ J. A. Abels and F. Moreno-Herrero and T. van der Heijden and C. Dekker and N. H. Dekker (2005). "Single-Molecule Measurements of the Persistence Length of Double-Stranded RNA". Biophysical Journal 88: 2737–2744. doi:10.1529/biophysj.104.052811.
- ^ L. J. Lapidus and P. J. Steinbach and W. A. Eaton and A. Szabo and J. Hofrichter (2002). "Single-Molecule Effects of Chain Stiffness on the Dynamics of Loop Formation in Polypeptides. Appendix: Testing a 1-Dimensional Diffusion Model for Peptide Dynamics". Journal of Physical Chemistry B 106: 11628–11640. doi:10.1021/jp020829v.
- O. Kratky, G. Porod (1949), "Röntgenuntersuchung gelöster Fadenmoleküle." Rec. Trav. Chim. Pays-Bas. 68: 1106-1123.
- J. F. Marko, E. D. Siggia (1995), "Stretching DNA." Macromolecules, 28: p. 8759.
- C. Bustamante, J. F. Marko, E. D. Siggia, and S. Smith (1994), "Entropic elasticity of lambda-phage DNA." Science, 265: 1599-1600. PMID 8079175
- M. D. Wang, H. Yin, R. Landick, J. Gelles, and S. M. Block (1997), "Stretching DNA with optical tweezers." Biophys. J., 72:1335-1346. PMID 9138579
- C. Bouchiat et al., "Estimating the Persistence Length of a Worm-Like Chain Molecule from Force-Extension Measurements", Biophys J, January 1999, p. 409-413, Vol. 76, No. 1